Table of Contents
Avalanche protection in Davos, Switzerland
Ana Stritih, Peter Bebi, Adrienne Grêt-Regamey
Protection from natural hazards such as avalanches is one of the most important ecosystem services provided by mountain forests. Forests decrease the probability of an avalanche release (Bebi et al. 2009), and reduce the mass and velocity of avalanches that flow through them (Feistl et al. 2014). The capacity of forests to provide avalanche protection depends on other side on their structure and species composition, which can be derived from EO data. On the other side, the demand for avalanche protection depends on the risk to human life and infrastructure, which can also be mapped using remote sensing. While data and models exist for some components of the avalanche protection system, they have not been integrated into a comprehensive model of the ecosystem service, and are associated with large uncertainties. We address this issue by developing a BN, which integrates existing models, EO data, and expert knowledge. The BN is used to more precisely map the ecosystem service and quantify the associated uncertainties (Stritih et al. 2019).
1. Developing the Bayesian Network
We based our avalanche protection model on previous models developed for this ES (Grêt-Regamey and Straub 2006, Grêt-Regamey et al. 2013) but extended it to incorporate newly available remote sensing inputs as well as recent developments in modelling forest-avalanche interactions. The BN structure was developed through an iterative process of literature review, consultation with experts, and testing the behaviour of the network with different input values.
The input nodes of the network are remote sensing variables, which are proxies for ecosystem structure, and in-situ or modelled avalanche data. These are linked to nodes that describe the natural hazard process, ecosystem functions, and demand for avalanche protection (based on a risk assessment approach).
Bayesian Network developed to model the ES of avalanche protection. The nodes are grouped and coloured based on the types of variables they represent. Spatial inputs are remote sensing and avalanche data, which are linked to variables describing ecosystem structure, avalanche hazard processes, ecosystem functions, and risk factors. The outputs of the network are the provision and demand for avalanche protection. Arrows represent causalities, not the flow of information, and are therefore oriented from ecosystem structure variables to the corresponding remote sensing inputs. Adapted from (Stritih et al. 2019).
2. Quantifying the network (CPTs)
In order to integrate different types of information (including remote sensing, process-based models, empirical models, and expert knowledge) and account for the associated uncertainties, we used a variety of methods to quantify the links between nodes in the network.
2.1 Links between remote sensing proxies and the actual state of the ecosystem
Remote sensing products (e.g. land cover classifications or LiDAR-based measurements of vegetation cover) represent a proxy of the actual state of the ecosystem. We make the uncertainty in the measurements or classifications explicit by creating separate nodes representing the observed value (Y) and the actual state (X) of the variable. The observation is caused by the actual state, not vice-versa, and defining the structure of the network based on this causality helps to define conditional probabilities.
We used this principle to account for uncertainties in the land cover classification. Classification errors are commonly expressed in confusion matrices, which contain counts of predicted classes for objects where the true class is known (in our case, obtained from 110 ground truth locations), with rows representing the classes in reality c, and columns representing the classes predicted by the classification (c’). Based on these counts, we can calculate either backward probabilities P(X = c | Y = c’) (e.g. the probability that a patch classified as forest is a forest in reality); or the forward probabilities P(Y = c’ | X = c) (that a forest patch will be classified as forest). The backward probabilities depend on the prior distribution of land cover – if we sample ground truth locations in a densely forested landscape, it is likely that many of the patches classified as forest will in fact be forested, leading to a higher backward probability than if we sample in a sparsely vegetated area. On the other hand, forward probabilities are inherent to the error process in the remote sensing data and the classification algorithm (Cripps et al. 2009), and are therefore consistent over the whole area. Therefore, we define the classification node Y as the child of the actual class X, and the rows of its CPT then correspond to the forward probabilities P(Y | X).
Confusion matrix of the land cover classification (a), the resulting CPT (b), and the resulting probability distribution when a pixel is classified as evergreen forest c.
For continuous remote sensing variables (such as the percentage of crown cover) with a known measurement error rate, we similarly define the measured cover Y as a child of the actual cover X. Assuming a normal distribution of errors, we define the conditional probability of Y as a normal distribution p(Y|X = x) = N(x, σ2) where the mean is the value of the actual state (x), and the standard deviation σ is defined by the measurement error. If we have no prior information about the actual state of X, a finding on the child Y (measurement) node then results in a normal distribution p(X|Y = y) = N(y, σ2) of the parent X (actual state). Since the error of lidar-based crown cover measurements was estimated to be 12 %, the CPT for lidar-measured crown was defined in Netica using the equation:
p(Crown_cover_Lidar | Crown_cover) = NormalDist(Crown_cover_Lidar, Crown_cover, 0.12*Crown_cover)
 Distribution of actual crown cover, given a measurement of crown cover. The CPT of Crown cover (Lidar) is defined as a normal distribution around the actual crown cover.
Distribution of actual crown cover, given a measurement of crown cover. The CPT of Crown cover (Lidar) is defined as a normal distribution around the actual crown cover.
2.2 Learning from process-based models
The process-based avalanche model RAMMS (Christen et al. 2010) simulates avalanche flows and also snow detrainment in forests during avalanches. In order to quantify the CPT of the node “Detrainment”, we simulated five known avalanche events in RAMMS with varying input parameters (e.g. different snow heights and parameters of snow erodibility, to account for uncertainty in the model). Then, we used the outputs of the simulations to “learn” the CPT of “Detrainment”, using the Expectation Maximisation algorithm in Netica.
2.3 Incorporating empirical models
Information on forests’ potential to prevent avalanches was available in the form of an empirical logistic model (Bebi et al. 2001). We included this model into the network using a Netica equation, including the model parameter uncertainty by incorporating the parameters not as single values, but as nodes with their probability distribution (normal distributions defined by the parameter estimates B and their standard errors). Then, we calculate the CPT of “Potential prevention” with an equation:
p (Potential_prevention | Slope, Gap_width, Crown_cover, Prevention_intercept, cover_B, slope_B, gap_B) = 1 - (logistic ((Prevention_intercept) + cover_B * Crown_cover + gap_B * Gap_width + slope_B * Slope))
However, this procedure results in a very large CPT for the node (a line for each combination of parameters and predictor variables). Since the parameter nodes will not be modified with evidence, we can reduce the CPT by using the function “Absorb nodes”, which removes the nodes from the network, but retains the associated information in the reduced CPT.
The parameters of an empirical model can be included explicitly as nodes in the network, to account for model uncertainty when calculating the CPT. Then, these nodes can be “absorbed” to reduce the size of the CPT.
2.4 Expert knowledge: linking quantitative variables to qualitative categories
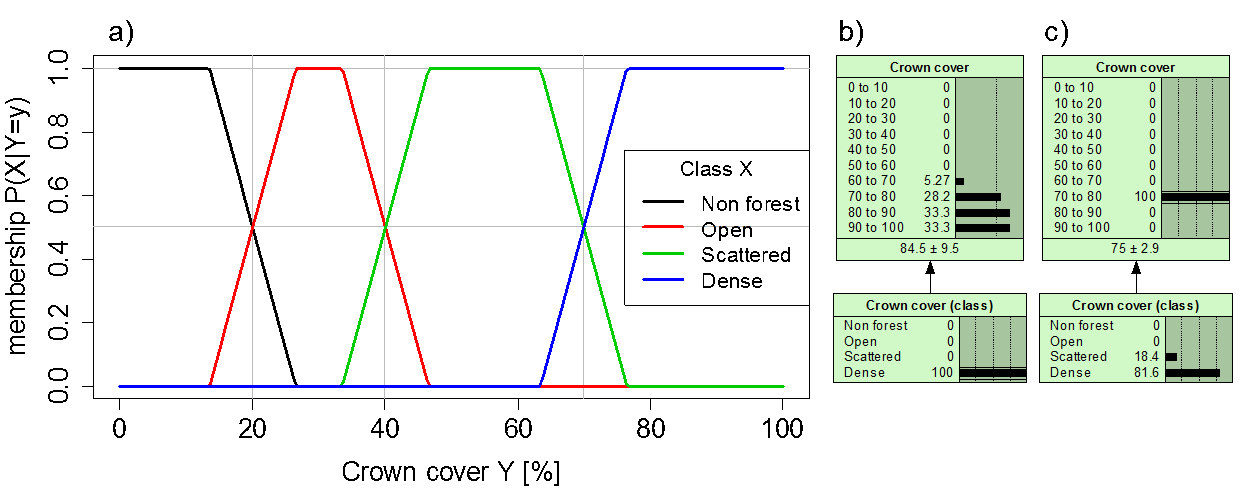
Expert knowledge is often related to qualitative categories rather than quantitative variables. For example, it may be easier for an expert to estimate the avalanche protection capacity of forests that are either “open”, “scattered”, or “dense”, rather than based on a percentage of crown cover. Linking such categories to numerical values is associated with a type of linguistic uncertainty (vagueness), where the delineation between categories is not sharp (Regan et al. 2002). Linguistic uncertainty is commonly addressed using fuzzy logic (Zadeh 1965), where membership functions m(y) define the level of membership (between 0 and 1) in a specific class for values of y. For example, we define trapezoidal membership functions of crown cover (Y) for the classes of forest density (X) (see figure below). The thresholds between classes have been defined by experts, whereas the slopes of the membership functions are defined based on the standard deviation of measured crown cover at locations where the forest density was classified in the field (method adapted from (Petrou et al. 2013)). At the expert-defined threshold of Y = 70 % crown cover, the probability of the forest being classified as “dense” is 0.5, while a forest with 100 % crown cover will certainly be classified as “dense” (P(X = dense) = 1). We use the membership function to define the probability of the class (X) given an observation y, P(X|Y=y), which is proportional to P(Y|X) * P(X).
An illustration of the use of fuzzy logic to translate quantitative variables to qualitative categories:: a) membership functions that define the classes of density based on the percentage of crown cover; b) probability distribution of crown cover for the class “dense”, based on the membership function; c) probability of classes when we observe a crown cover of 70 %.
2.5 Expert knowledge: estimating distributions
For nodes where no data was available (e.g. “Potential detrainment”), we used expert knowledge to quantify the CPT. To avoid overconfidence, we used the “four-point estimation method” (Speirs-Bridge et al. 2010), where we asked the expert to estimate the lowest and highest value they would expect, the most likely value, and their confidence that the true value is within this range (Metcalf and Wallace 2013). For example, for a dense evergreen forest on rough terrain, the expert estimated the lowest possible detrainment factor to be 24 Pa, the highest 96 Pa, and the best estimate at 48 Pa, with a confidence of 80%. This gives us the quantiles and mode of the distribution, to which we fitted a simple asymmetric triangular distribution (see figure below).
Expert-based distribution of potential detrainment for a dense evergreen forest on rough terrain.
3. Spatial application
The spatial inputs to the avalanche protection BN are remote sensing variables, including a land cover classification (derived from a combination of Sentinel2 and aerial LiDAR data) and variables derived from high-resolution aerial LiDAR, such as crown cover, terrain roughness, and detected buildings. In addition, modelled avalanche velocities under two scenarios, extreme (300-year) and frequent (30-year), provide information on the spatial patterns of the avalanche hazard. Using raster inputs, we performed inference for each pixel in a 5 m resolution raster of the study area. Since the provision and demand for avalanche protection do not occur at the same location, and spatial processes could not be modelled in the pixel-based BN, we quantified provision and demand separately. Thus, we obtained posterior probability distributions of avalanche protection provision and demand for each pixel. In order to map the outputs, we calculated the per-pixel median and entropy (uncertainty) of the posterior probability distributions.
 Modelled provision of avalanche protection in the Dischma valley (5 m resolution). The value is expressed in m of snow, while the uncertainty is calculated as the entropy of the posterior probability distribution. Most areas with a high value of the service also have a high uncertainty (dark red), as do some forested areas with a predicted low protection value (dark blue). Only areas with a zero or very low (light blue) value of the service show a high certainty. From (Stritih et al. 2019).
Modelled provision of avalanche protection in the Dischma valley (5 m resolution). The value is expressed in m of snow, while the uncertainty is calculated as the entropy of the posterior probability distribution. Most areas with a high value of the service also have a high uncertainty (dark red), as do some forested areas with a predicted low protection value (dark blue). Only areas with a zero or very low (light blue) value of the service show a high certainty. From (Stritih et al. 2019).
4. Validation and sensitivity analysis
The model and the resulting maps of avalanche protection provision and demand, as well as the underlying ecosystem functions, were presented and discussed with local experts. In addition, we performed a sensitivity analysis of the model, using the Netica function “Sensitivity to findings” to calculate the reduction of entropy (uncertainty) on the target nodes in response to findings on other nodes in the network. The entropy reduction (also called mutual information) gives us an indication of which variables in the system have the highest influence on the ecosystem service.
We also performed a stepwise sensitivity analysis to visualize the flow of information in the network. For each node X, we calculated the proportion of its entropy that can be reduced by a finding on each of its parents. These relative mutual information values were used as weights for links between nodes in a Sankey diagram of the network (see figure below). For each node, the thickness of incoming (from the left) links show how much the entropy on the node can be reduced by findings on preceding nodes. Mutual information is not additive, i.e. if both parent nodes can reduce the entropy of a child by 50%, this does not mean that findings on both parents will result in complete certainty on the child node. Nonetheless, plotting the MI gives an indication of the main sources of uncertainty in the model. When the value of MI for all the parents of a node is rather low, this means that the node will have a wide probability distribution even when the states of its parents are known, implying high uncertainty in the corresponding links. If such a node has a large influence on the outcome of the network, this indicates a knowledge gap.
Stepwise sensitivity analysis of the BN, where the width of a link between two nodes corresponds to the relative mutual information (MI %), i.e. the percentage of the entropy on a node that can be reduced by a finding on a preceding node. The nodes are labelled and coloured by the type of variable represented (see Fig 6.1-1), while the link colours represent the types of uncertainty taken into account while quantifying the link in the BN. From (Stritih et al. 2019).
Overall, the uncertainties related to avalanche processes contribute more to the final uncertainty in ES provision than uncertainties about ecosystem structure. For example, the node “Release” (describing whether a pixel is in a potential avalanche release area) has an important influence on subsequent nodes in the network, but findings on its parents (“Slope”, “Roughness (measured)” and “Curvature”) can only reduce a small part of its entropy, so it is a major source of uncertainty in the model. Some remote sensing inputs have a strong effect on the knowledge about ecosystem structure (“Gap width” and “Crown cover”), while others have higher uncertainty (e.g. “Roughness”). There is high uncertainty in land cover classification, as its mutual information with actual land cover is only 29 %. However, additional information on actual land cover is gained from the crown cover class (MI = 59 %). The links from ecosystem structure to the potential provision of ES also contain high uncertainty, regarding both the potential of a forest to prevent avalanches (empirical model-based “Potential prevention”) and to stop snow during an avalanche (expert-based “Potential detrainment”). However, “Potential detrainment” has a relatively low influence on the corresponding ecosystem function (process model-based “Detrainment”). This function is affected more strongly by the avalanche process (“Velocity”), which in turn is affected by the natural variability in release conditions (“Max new snow height”).
5. Description of the network nodes
| Node | Description | States | CPT method |
|---|---|---|---|
| Input nodes - remote sensing | |||
| Land cover classification | Random forest classification with combination of LiDAR, aerial CIR images and Sentinel2 | Evergreen forest, deciduous forest, non-forest | Confusion matrix |
| Crown cover (measured) | Measured cover of vegetation above 3 m | 10 states: 0 - 100 [%] | Normal distribution around actual state |
| Roughness (measured) | Measured terrain roughness, derived from LiDAR-based DTM (Sappington et al., 2007) | 9 states: 0 - 1 | Fuzzy definition of categories based on ground truth |
| Gap width (measured) | Width (along contour lines) of non-forested area [m], derived from LiDAR-based CHM | 9 states: 0 - 8000 [m] | Normal distribution around actual state |
| Building (detected) | Presence of a building detected from LiDAR | Boolean | Confusion matrix |
| Curvature | Planar slope curvature, derived from LiDAR-based DTM | 7 states: -45 - 5 | |
| Slope | Slope angle, derived from LiDAR-based DTM | 8 states: 0 - 90 [°] | |
| Elevation | Elevation [m a.s.l.] | 7 states: 1500 - 2900 | |
| Input nodes - avalanche hazard data | |||
| Max new snow height | Annual maximum new snow height, which determines the avalanche release scenario | 9 states: 0 - 2 [m] | Gumbel distribution of maximum new snow height, Davos, Fluelastrasse |
| Velocity 300 | Maximum velocity under the 300 year scenario, modelled in RAMMS | 9 states: 0 - 60 [m/s] | |
| Velocity 30 | Maximum velocity under the 30 year scenario, modelled in RAMMS | 10 states: 0 - 60 [m/s] | |
| Nodes representing ecosystem structure | |||
| Crown cover | Cover of vegetation above 3 m | 10 states: 0 - 100 [%] | Fuzzy logic definition of categories |
| Crown cover (class) | Category of forest density | Dense, scattered, open, non-forest | |
| Roughness (class) | Category of terrain roughness | Rough, knobby, smooth | |
| Land cover | Actual land cover class | Evergreen forest, deciduous forest, non-forest | Based on ground truth plots |
| Gap width | Width (along contour lines) of non-forested area [m] | 9 states: 0 - 8000 [m] | |
| Potential release prevention | Potential of forest to prevent an avalanche release | Boolean | Logistic mode (Bebi et al., 2001)l |
| Potential detrainment | Capacity of forest to remove snow from avalanche flow | 12 states: 0 - 120 [Pa] | Expert knowledge (four-point estimation) |
| Nodes representing the hazard process | |||
| Release | Probability of an avalanche release | Boolean | Fuzzy logic |
| Release height | Height of snow released in the event of an avalanche | 10 states: 0 - 3 [m] | Logical combination of “Release” and “Max new snow height”, corrected for “Slope” |
| Velocity | Maximum avalanche flow velocity | 9 states: 0 - 60 [m/s] | Defined by scenarios, with uncertainty estimated based on simulations with varying input parameters |
| Max pressure | Maximum avalanche pressure | 4 states: = 0 - 300 [kPa] | Derived from velocity, with uncertainty estimated based on simulations with varying input parameters |
| Nodes representing ecosystem functions | |||
| Release prevented | Probability a release would be prevented by the forest | Boolean | Logical combination of “Release” and “Potential prevention” |
| Prevention | Height of snow in prevented avalanche release | 11 states: 0 - 3 [m] | Logical combination of “Release prevented” and “Release height” |
| Detrainment | Height of snow detrained in forest during avalanche | 7 states: 0 - 0.8 [m] | Learning from RAMMS simulations with varying input parameters |
| Risk assessment and valuation nodes | |||
| Building | Presence of a building | Boolean | |
| Building type | Type of building | One-family house, farm building, guesthouse, multi-family house, industrial, infrastructure | Distribution of types from local data |
| Lethality | Avalanche pressure is lethal | Boolean | Fuzzy logic based on values from literature (Swiss National Platform for Natural Hazards) |
| People per building | Average no. of people per building | 6 states: 0 - 20 | Fuzzy logic based on values from literature |
| People present | People are present in a building | Boolean | Fuzzy logic based on values from literature |
| Damage | Building is destroyed by avalanche | Boolean | Fuzzy logic based on values from literature |
| Building cost | Cost of destroyed building | 6 states: 0 - 10`7 [CHF] | Distribution per type from local data |
| Damage (cost) | Cost due to damaged building | 7 states: 0 - 10`7 [CHF] | Logical combination of “Damage” and “Building cost” |
| Cost of human death | Constant: 5*10`6 [CHF] | Constant value from literature, Life Quality Index approach (Merz et al. 1995) | |
| Lethality (cost) | 5 states: 0 - 10`8 [CHF] | Logical combination of “Lethality” and “Cost of human death” | |
| Output nodes | |||
| Provision | Combination of prevented release and detrained snow height | 12 states: 0 - 4 [m] | Sum of “Prevention” and “Detrainment” |
| Demand | Avalanche risk to people and buildings | 5 states: 0 - 1.1*10`8 [CHF] | Sum of “Damage (cost)” and “Lethality (cost)” |